Ермакова Е.С., Румянцева И.Б., Целищева И.И. Развитие гибкости мышления детей дошкольного возраста с использованием комбинаторных заданий
В исследованиях Е.С. Ермаковой показано, что гибкость мышления как значимый компонент творческого мышления проявляется уже в дошкольном возрасте и начинает бурно развиваться к 5-6 годам, хотя без специального обучения не достигает у большинства детей высокого уровня развития. «Структуру гибкости мышления составляют ее средства — специфические представления, а также мыслительные действия, позволяющие оперировать ими» [1, с. 17]. Мыслительные действия включают анализ признаков объекта, ориентировку на существенные в данной ситуации признаки, выявление различия и сходства, причинно-следственных связей и зависимостей, установление закономерностей.
По нашему мнению, стратегия формирования гибкости мышления детей, основанная на активизации представлений и развитии мыслительных действий, предусматривает преемственность в организации образовательной деятельности детей. «На первом этапе обучения детей необходимо учить последовательности анализа признаков объекта, когда дети выделяют все более и более скрытые, неочевидные свойства и одновременно синтезируют многоплановый образ данного объекта. На следующем этапе требуется учет признаков в системе связей объекта, их переориентировка, обобщение по различным основаниям, в зависимости от условий задачи» [3, с. 17].
В исследованиях Е.С. Ермаковой установлено, что гибкость мышления в соответствии с выделенными этапами можно формировать у детей начиная с 4 лет [1]. Особенно эффективными для ее развития являются математические задачи, позволяющие анализировать различные для разных ситуаций основополагающие свойства и связи объектов. Именно математические представления являются теми представлениями, в которых обобщенно структурируются свойства, связи и отношения предметов и явлений и на основе которых возникают научные понятия. Подобным требованиям удовлетворяют комбинаторные задания и задачи. Они характеризуются как задания, требующие выбора из некоторого заданного множества его подмножества в том или ином порядке. Здесь имеются в виду не разные способы нахождения одного и того же ответа, а существование разных решений — ответов и их поиск. Особенностью данных задач является то, что их решения не укладываются в рамках обычной схемы. Дети должны предложить несколько решений задачи. Такие задачи не сковывают жесткими рамками одного решения, а открывают возможность для поисков и размышлений, способствуя развитию гибкости детского мышления.
Включение комбинаторных заданий в обучение детей от случая к случаю не позволяет решить проблему развития гибкости мышления. В основе системы обучения детей выполнению комбинаторных заданий лежат следующие принципы:
• психологическое содержание обучения составляет стратегия развития гибкости мышления детей (следование этапам ее формирования);
• учет процесса интериоризации (первоначальное выполнение комбинаторных заданий детьми в практической деятельности, затем перенесение практических действий через речевые действия в план умственных действий);
• тесная связь содержания комбинаторных заданий с основным содержанием начального курса математики в соответствии с образовательными стандартами для детей дошкольного и младшего школьного возраста;
• последовательное использование метода перебора с целью обучения рациональным приемам систематического перебора как основы для введения в дальнейшем комбинаторных правил и формул.
Нами разработаны методические рекомендации, показывающие как на практике реализовать данные принципы в системе развивающего обучения детей дошкольного и младшего школьного возраста [2-4].
Как отмечалось выше, комбинаторные задания и задачи выполняются детьми дошкольного возраста на основе практических действий путем перебора. Перебор может предусматривать обнаружение как всех возможных комбинаций с объектами, так и лишь их части, удовлетворяющей условиям, заданным в задаче. Проиллюстрируем данный этап обучения детей в возрасте 4-7 лет решению комбинаторных задач на примере комплекса следующих развивающих заданий.
Задание 1. «Поможем выбрать рыбок»
В магазине продавали 5 больших рыбок и 4 маленьких рыбки. Слава хочет купить для своего аквариума 2 большие рыбки и 1 маленькую. Какие наборы рыбок может сделать Слава?
Методические рекомендации.
Педагог (П). Ребята, к нам за помощью обратился мальчик Слава. Он пошел в зоомагазин, чтобы купить рыбок, но не знает, какому набору рыбок отдать предпочтение. Поможем ему выбрать рыбок?
Педагог формулирует задачу: «В магазине продавали 5 больших рыбок и 4 маленьких рыбки. Слава хочет купить для своего аквариума 2 большие рыбки и 1 маленькую. Какие наборы рыбок может сделать Слава? »
П. Чем удобнее заменить рыбок, чтобы составить Славе наборы для покупки? Как показать, что рыбки разные?
У детей на партах карандаши красного, синего, зеленого, желтого и оранжевого цветов.
П. Изобразите 5 больших рыбок и 4 маленьких.
Дети, используя разные цвета, рисуют овалы (рис. 1).

Далее дети зарисовывают несколько наборов из трех рыбок: 2 большие и 1 маленькая.
Примечание: всего может быть составлено 40разных наборов. Задание считается правильно выполненным, если оно удовлетворяет заданному условию: в наборе должно быть 2 большие рыбки и 1 маленькая.
П. Каких же рыбок мог купить Слава в магазине? Какой набор сделал ты? Почему?
Отвечая на поставленные вопросы, дети убеждаются, что наборы могут быть разными. Важно, чтобы в наборе было 2 большие рыбки и 1 маленькая, а виды рыбок могут быть разными.
П. Слава удивляется, почему он не мог сразу сделать такой выбор. Потому что таких вариантов выбора много. Он благодарит вас за помощь и обещает подумать, какой из предложенных вами наборов ему выбрать.
Задание 2. «Разберем завал из камней»
В игровой ситуации детям предлагают разобрать завал из камней на тропинке, по которой они идут. Дети обнаруживают, что каждый камень обладает четырьмя признаками (форма, размер, цвет, характер поверхности). В качестве моделей камней можно использовать геометрические фигуры, вырезанные из гладкой и бархатной бумаги. Камни различаются по форме (круглые и овальные), размеру (большие и маленькие), цвету (светлые и черные), по поверхности (гладкие и шершавые). Их предлагается разложить
слева и справа от тропы разными способами так, чтобы в каждой куче были похожие.
Задание 3. «Разделим рыбок на группы»
Рассадите семь рыбок, различающихся размером, цветом, формой хвоста и плавника, в два аквариума разными способами.
Методические рекомендации.
П. Сегодня, ребята, мы отправимся в зоомагазин, где продаются рыбки. Они такие же, как и модели, которые лежат у вас на столах.
Сколько всего рыбок вы видите? (Рис. 2.)
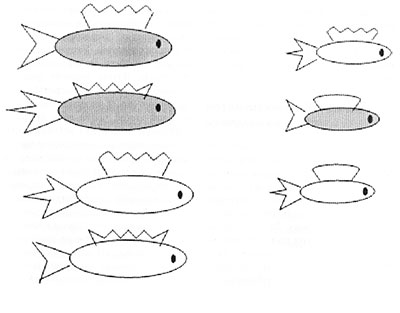
Дети. Семь. Всего семь рыбок.
Педагог предлагает детям разделить рыбок на группы так, чтобы в одну группу попадали рыбки, чем-то похожие друг на друга. Дети выполняют задание, ориентируясь на какой-либо признак. Они могут разбить рыбок на группы по цвету (светлые и темные), по размеру (большие и маленькие), по форме хвоста
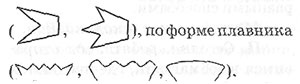
Все варианты внимательно выслушиваются.
Задание 4. «Разделим пирог»
Педагог раздает каждому ребенку модель пирога. Пирог имеет квадратную форму. Детям предлагается разделить его по-разному на четыре равные части. Какой формы могут получиться части?
Задание 5. «Конструируем из палочек»
Педагог раздает каждому ребенку по 5 палочек и предлагает построить с помощью этих палочек флажок. Форма флажка не указывается, поэтому дети могут получить флажки, разные по форме (треугольные и квадратные). Затем педагог предлагает из этих палочек изобразить то, что они сами желают. Дети могут изобразить домик, лесенку, заборчик, стул и другие объекты.
Педагог раздает каждому ребенку лист, на котором нарисованы 5 рыбок (в изображении каждой рыбы есть тело, хвост и верхний плавник). Из коробки карандашей (или фломастеров) детям предлагается выбрать три карандаша разных цветов. С помощью этих трех карандашей необходимо раскрасить рыбок разными способами. Сочетая по-разному цвета тела, плавника и хвоста, дети выполняют предложенное задание.
Задание 7. «Поможем садовнику»
Педагог показывает детям коробку с квадратным основанием, разделенную перегородками на 9 равных частей. Уточняет, что в такую коробку можно положить 9 плодов. Затем педагог раздает каждому ребенку квадраты, разделенные на 9 равных частей. В каждой такой части есть прорезь, в которую дети будут вставлять фигурки плодов. Педагог формулирует задание: «Садовник просит нас разложить в коробки яблоки, сливы и груши так, чтобы в каждой коробке расположение плодов было разное, и у каждой стенки лежали три разных плода, и в каждом ряду, и в каждом столбике расположение плодов не повторялось». (Плоды заменяются геометрическими фигурами разного цвета: круг, овал, треугольник.)
Задание 8. «Сварим компот»
Для компота купили яблоко, грушу, сливу, черешню. Необходимо отобрать для компота только три из четырех купленных продуктов. Сколько разных наборов можно сделать из этих четырех продуктов, если брать по три? Сколько разных компотов получится?
Методические рекомендации.
Дети заменяют фрукты и ягоды геометрическими фигурами и составляют наборы, учитывая указанное в задании условие. Затем все наборы сравниваются, чтобы выделить среди них различные. Дети убеждаются, что можно сварить четыре различные по составу компота. Аналогично можно организовать творческую деятельность при выполнении заданий «Приготовим салат из овощей», «Сварим суп» и др.
Задание 9 «Меню для крольчихи»
Педагог предлагает решить задачу: «Даша приехала в деревню к бабушке и дедушке. У них жила большая крольчиха. Бабушка с дедушкой приготовили ей в качестве корма на неделю четыре морковки разного размера и три кочана капусты разных размеров. Бабушка сказала Даше, что эти овощи нужно давать крольчихе в течение недели. Для этого она попросила Дашу составить овощное меню на одну неделю для крольчихи».
Методические рекомендации.
Педагог организует беседу с детьми по следующему плану:
П. Сколько дней в одной неделе? Как они называются по порядку?
Дети вспоминают названия дней недели. Педагог на доске, а дети в тетради записывают в столбик названия дней недели, указывая первую букву каждого дня недели.
П. Чем удобно заменить морковь?
Дети (Д.). Треугольниками.
П. Нарисуйте под таблицей нужное количество треугольников. Подумайте, какого они должны быть размера, если морковки все были разной величины.
Дети рисуют четыре треугольника разных размеров.
П. Чем можно заменить капусту?
Д. Кругами.
П. Нарисуйте нужное число кругов. Учитывайте, что кочаны были разной величины.
Дети рисуют три круга разных размеров.
П. Сколько овощей нужно давать крольчихе каждый день, чтобы их хватило на целую неделю (на 7 дней)?
Д. Овощей семь и дней семь. Значит, надо давать по одному овощу.
П. Составьте меню для крольчихи.
Дети зарисовывают около записанных в тетради букв круги и треугольники. Педагог проверяет.
П. Посмотрите на меню соседа по парте. Сравните ваши меню. Чем отличается его меню от вашего? Какой вывод можно сделать?
Дети делают вывод, что меню у всех получились разные, что можно составить много овощных наборов, и убеждаются, что каждый из них является правильным решением задания.
Задание 10. «Меню для кошки»
Педагог предлагает выполнить задание: «Составьте меню для кошки на три дня, учитывая, что сутки можно разделить на 4 части (утро, день, вечер ночь) и чтобы меню на каждый день было разным».
Педагог демонстрирует учащимся карточки, на которых изображены продукты для кормления кошки. Например: хлеб, молоко, рыба, готовый сухой корм, сметана, каша, яйцо, мясо, вода. Каждый ребенок вписывает в таблицу свой вариант меню для кошки на три дня.
Дети сравнивают получившиеся меню. Обсуждают, почему у них осталась незаполненной последняя колонка, убеждаясь, что разных способов составления меню существует много, но каждое из них может быть признано правильным решением задачи. Перед детьми не ставится задача составления всех возможных меню.
Задание 11» «Покормим рыбок»
В начале игры дети вспоминают, чем человек кормит разных аквариумных рыб. Педагог выписывает название корма на доску: мотыль, хлеб, каша, сухой корм, яичный желток. Затем педагог предлагает составить меню для рыбок на неделю, если каждый день можно давать только два вида корма. И сочетания кормов в течение недели не должны повторяться. Дети вспоминают названия дней недели и договариваются записывать меню в таблицу.
У каждого ребенка получается свое меню. Педагог с помощью интерактивной доски демонстрирует все возможные варианты наборов. Дети ищут свой вариант и радуются. Все подсчитывают число таких вариантов. Их получается 10. Дети делают вывод, что данное задание имеет много вариантов правильных решений.
Задание 12. «Разбиваем клумбу»
Мама дала дочке задание отметить ямки для посадки пяти цветов на клумбе прямоугольной формы. Девочка отметила две ямки внизу и три внизу клумбы. Она думает, что есть и другие варианты. Кто из вас может предложить другие варианты посадки цветов?

Методические рекомендации.
Дети получают листок бумаги с обозначенной клумбой — рабаткой (длинная прямоугольная клумба). Карандашом дети отмечают ямки для посадки цветов. Важно, чтобы ямок для посадки было пять. Их расположение не играет роли. Возможны следующие варианты:
Представленные комбинаторные задания имеют интегрированный характер, так как в процессе их выполнения дети в синтезе применяют свои природоведческие и математические представления. Например, при составлении упорядоченных или неупорядоченных наборов из элементов предметного множества дети применяют представления об особенностях кормления домашних животных (кроликов и кошек), аквариумных рыбок и др. В этих же заданиях они применяют знания названий частей суток, дней недели, месяцев, времен года. Выполняя количественный или порядковый счет элементов предметного множества, дети используют знания определенных признаков, входящих в определенное понятие (например, понятие «рыбы»). Это способствует формированию у детей целостных представлений об окружающем мире. Педагоги, организующие образовательную деятельность детей дошкольного возраста по нашей авторской программе «Математика вокруг нас» [5-7], активно используют представленные в статье задания и подобные им [2, 3]. Поэтому мы на практике убедились, что комбинаторные задания практической направленности доступны для выполнения детям дошкольного возраста начиная с 4 лет. Они важны для развития познавательной мотивации, внимания, памяти, связной объяснительной речи дошкольников и формирования важнейшего компонента творческого мышления — гибкости.
Список литературы
1. Ермакова Е.С. Психологические закономерности формирования гибкости продуктивного мышления у детей дошкольного и младшего школьного возраста: Автореф. дис. ... докт. пси-хол. наук. СПб., 2006. 42 с.
2. Ермакова Е.С, Румянцева И.Б., Целищева И.И. Обучение решению комбинаторных задач детей 4-10
лет // Начальная школа. 2005. № 11. С.83-91.
3. Ермакова Е.С, Румянцева И.Б., Целищева И.И. Возможности комбинаторики для развития гибкости мышления у дошкольников // Начальная школа плюс До и После. 2008. № 2. С. 17-23.
4. Ермакова Е.С, Румянцева И.Б., Целищева И.И. Развитие гибкости мышления детей. Дошкольный и младший школьный возраст: Учеб.-метод, пос. СПб.: Речь, 2007. 210 с.
5. Целищева И.И., Румянцева И.Б. Математика вокруг нас: средняя группа ДОУ. М.: ИЛЕКСА, 2008. 92 с.
6. Целищева И.И., Румянцева И.Б. Математика вокруг нас: старшая группа ДОУ. М.: ИЛЕКСА, 2008. 130 с.
7. Целищева И.И., Румянцева И.Б. Математика вокруг нас: подготовительная группа ДОУ. М.: ИЛЕКСА, 2012. 138 с.
д.психол.н., профессор кафедры прикладной психологии Петербургского университета путей сообщения Императора Александра I
И.Б. РУМЯНЦЕВА
к.психол.н., доцент кафедры математики, физики и методики обучения Шуйского филиала ФГБОУ ВПО «Ивановский государственный университет»
И.И. ЦЕЛИЩЕВА
доцент кафедры математики, физики и методики обучения Шуйского филиала ФГБОУ ВПО «Ивановский государственный университет»
"Одаренный ребенок" . - 2015 . - № 5 . - С. 92-100.





 Издательство «Свиньин и сыновья» выпустило несколько сотен самых разных по жанру, объему и авторам, но неизменно высококультурных изданий
Издательство «Свиньин и сыновья» выпустило несколько сотен самых разных по жанру, объему и авторам, но неизменно высококультурных изданий





